Bem vindo à revisão de álgebra linear. Aqui irei mostrar o básico de álgebra linear, tentando . Esse tutorial foi feito visando os fundamentos para os tutoriais de WebGL, mas podem ser usados em qualquer outra aplicação.
Vetores
Um vetor é uma tupla \([x_1,x_2, ...,x_n]\), com \(x_i \in R^n, 1 \le i \le n\). É uma entidade geométrica com magnitude, direção e sentido. Ela pertence a um conjunto denominado espaço vetorial. Nesse conjunto, se dois vetores tiverem a mesma magnitude, direção e sentido, então elas são iguais. Um vetor não tem posição definida, então não faz sentido transladar um vetor (ela pode estar em qualquer lugar). O valor de \(n\) é a dimensão do vetor. Um vetor como
\[\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\]
é um vetor coluna. Um vetor \([1,2,3]\) é um vetor linha. A transposta de um vetor coluna é um vetor linha. Para economizar espaço, poderemos tratar um vetor coluna como \([1,2,3]^T\). Outra notação é tratar um vetor \(\vec{a}\) como \([a_1,a_2,a_3,a_4]\) ou \([a_x,a_y,a_z,a_w]\).
Um ponto também é uma tupla \((x_1,x_2, ...,x_n)\), com \(x_i \in R^n, 1 \le i \le n\). Veja que estamos usando a notação \(()\) para ponto e \([]\) para vetor, mas isso pode mudar nos livros-texto. Geralmente um ponto representa uma posição, ao invés de um deslocamento.
Mas um vetor não é a mesma coisa que um ponto? Em termos numéricos, sim, mas em termos semânticos, não. Veja algumas diferenças:
| ponto | vetor |
|---|---|
| representa uma posição | representa um deslocamento |
| não tem direção | tem direção |
| não tem sentido | tem sentido |
| não tem magnitude | tem magnitude |
| tem posição | não tem uma posição específica |
Quando quiseres especificar uma posição, por exemplo um lugar A com latitude=-23 e longitude=-46, especificas um ponto (-23, -46). Quando quiseres especificar um deslocamento, por exemplo entre A(-23, -46) e B(50, 20) precisas caminhar 73 unidades no eixo X e 66 unidades no eixo Y, resultando em [73,66], que é diferente de um ponto C na posição (73,66).
Geometricamente podemos associar pontos e vetores:
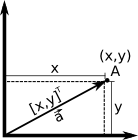
Matematicamente podemos associar pontos e vetores dessa forma:
- \(A - B = \vec{v}\)
- \(A + \vec{v} = B\)
- \(\vec{v} + \vec{w} = \vec{z}\)
Vetor zero
A identidade da operação de adição entre vetores é o vetor zero: \([0,0,\dots,0]^T\). Se fixares a magnitude de um vetor, todos os vetores distintos formam um círculo de vetores. Porém o vetor zero não tem direção, ou seguindo a definição, tem todas as direções. Não pense no vetor zero como um ponto, pense como "sem deslocamento".
Negar um vetor
\(-\vec{a}= -[a_1,a_2,\dots,a_n]^T = [-a_1,-a_2,\dots,-a_n]^T\)
Geometricamente invertes o sentido do vetor:
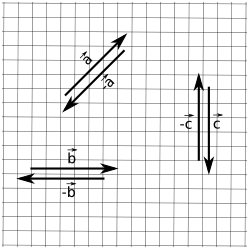
Magnitude
A magnitude, também conhecido como norma, comprimento ou intensidade, não está explícito no vetor. O vetor \([3,4]^T\) tem magnitude nem 3 nem 4, mas 5. Veja como calculá-lo:
\(\|v\| = \sqrt{v_1^2 + v_2^2 + ... + v_{n-1}^2 + v_n^2}\)
\(\|v\| = \sqrt{\sum^{n}_{i=1}{v_i^2}}\)
Geometricamente, usando pitágoras:
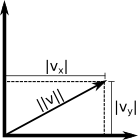
\(v_x\) e \(v_y\) podem ser valores negativos, todavia \(\|v\|\) não é. Já que \(|x|^2 = x^2\) então as equações seguintes são equivalentes:
- \(\|v\|^2 = |v_1|^2 + |v_2|^2\)
- \(\|v\|^2 = v_1^2 + v_2^2\)
Multiplicação por um escalar
\[ k \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} k = \begin{bmatrix} kv_1 \\ kv_2 \\ \vdots \\ kv_n \end{bmatrix} \]
Dividir por k é igual a multiplicar por \(\frac{1}{k}\). Algumas observações:
- Geralmente multiplicação entre escalar e vetor não tem símbolo de multiplicação;
- multiplicação entre escalar e vetor ocorre antes de adição: \(3\vec{a} + \vec{b}\) é o mesmo que \((3\vec{a})+\vec{b}\), mas diferente de \(3(\vec{a}+\vec{b})\);
- Um escalar não pode ser dividido por um vetor, e um vetor não pode ser dividido por outro vetor;
- Negação de vetor pode ser visto como multiplicação pela escalar -1.
Geometricamente, a multiplicação de um vetor por uma escalar estica ou encolhe o vetor, mantendo seu sentido e direção, mas mudando sua magnitude proporcionalmente à escalar:
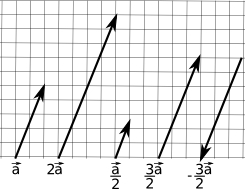
Normalização
Multas vezes só queres saber o sentido do vetor, sem se importar com a magnitude:
- Para onde o vento está orientado nesse ponto?
- Para onde esse fóton está indo?
- Essa cidade fica ao norte ou ao leste daqui?
- Na sinuca, em que direção o taco deve se orientar para acertar a bola?
Podemos representar estas situações com um vetor unitário (sua magnitude é igual a 1), também chamado de versor ou normal. Podemos obter um versor de um vetor dividindo-o pela sua magnitude:
\(\vec{v}_{norm} = \frac{\vec{v}}{\|v\|}\)
Por causa do denominador, não podemos obter o versor do vetor zero.
Geometricamente:

Adição e Subtração de vetores
Na adição, \(\vec{a} + \vec{b} = \vec{b} + \vec{a}\):
\[ \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} = \begin{bmatrix} a_1 + b_1 \\ a_2 + b_2 \\ \vdots \\ a_n + b_n \end{bmatrix} \]
Na subtração, \(\vec{a} - \vec{b} = - (\vec{b} - \vec{a})\):
\[ \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} - \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} = \begin{bmatrix} a_1 - b_1 \\ a_2 - b_2 \\ \vdots \\ a_n - b_n \end{bmatrix} \]
Geometricamente:
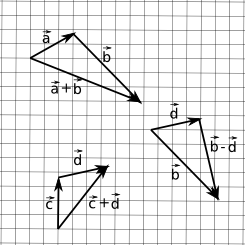
Uma forma de ver estas operações:
- Adição: se eu caminhar por uma sequência de lugares, qual o deslocamento do primeiro lugar para o último?
- Subtração: se eu sair daqui para um dos dois outros lugares, qual é o deslocamento entre estes destinos? É longe um do outro?
Perceba que eu posso representar um vetor como uma sequência de deslocamentos (uma adição) de versores:
\[ \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} = a_1\begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} + a_2\begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} + \dots + a_n\begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} \]
Distância entre pontos
Dados dois pontos A e B, podes obter um vetor \(v = A-B = [a_1 - b_1,a_2-b_2,\dots,a_n-b_n]^T\). A distância entre A e B é a magnitude \(\|v\| = \sqrt{(a_1-b_1)^2+(a_2-b_2)^2+\dots+(a_n-b_n)^2}\)
Produto Escalar
Vimos como multiplicar um vetor por um produto escalar. Podemos multiplicar um vetor por um outro vetor. Com o tempo, perceberam que certas formas de multiplicação entre vetores tornaram-se úteis no dia-a-dia.
O produto escalar (ou produto interno) tem esse nome pois o resultado é uma escalar. Dado dois vetores \(\vec{a}\) e \(\vec{b}\), o produto escalar \(\vec{a}\cdot\vec{b} = a_1b_1 + a_2b_2 + \dots + a_nb_n\). Simplesmente é a multiplicação elemento a elemento. Qual a utilidade disso. Fica mais fácil vendo geometricamente a consequência dessa operação:
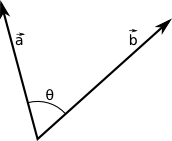
O produto escalar retorna o quão similar é um vetor do outro. Se eles forem perpendiculares, o valor do produto escalar é 0. Outra fórmula para o produto escalar é:
\(\vec{a}\cdot\vec{b} = \|\vec{a}\|\|\vec{b}\|cos(\theta)\)
Produto escalar entre versores é mais simples (dado versores \(\vec{a}\) e \(\vec{b}\):
\(\vec{a}\cdot\vec{b} = cos(\theta)\)
Projetando um vetor no outro
Digamos que tenhas modelado um coqueiro inclinado e o sol esteja exatamente acima, e queiras projetar sua sombra. Representando estas elementos como vetores:
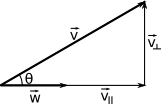
Precisamos decompor \(\vec{v}\) em dois vetores: \(\vec{v}_\parallel\) (paralelo a \(\vec{w}\)) e \(\vec{v}_\perp\) (perpendicular a \(\vec{w}\)), de forma que \(\vec{v}_\parallel + \vec{v}_\perp = \vec{v}\). Usando os conceitos trigonométricos aprendidos na escola primária e secundária, sabemos que
\[\|\vec{v}_\parallel\| = \|\vec{v}\|cos(\theta)\].
Mas neste tutorial aprendemos que
\[\vec{v}\cdot\vec{w} = \|\vec{v}\|\|\vec{w}\|cos(\theta)\]
\[\|\vec{v}\|cos(\theta) = \frac{\vec{v}\cdot\vec{w}}{\|\vec{w}\|}\]
Assim podemos fazer a relação entre \(\vec{v}\) e \(\|\vec{v}_\parallel\|\) sem precisar do ângulo:
\[\|\vec{v}_\parallel\| = \frac{\vec{v}\cdot\vec{w}}{\|\vec{w}\|}\]
Ou seja, já temos a magnitude de \(\vec{v}_\parallel\). E se eu quiser de fato o \(\vec{v}_\parallel\)? Podemos criar um versor de \(\vec{w}\) e multiplicá-lo pela magnitude de \(\vec{v}_\parallel\):
\[\vec{v}_\parallel = \frac{\vec{w}}{\|\vec{w}\|}\|\vec{v}_\parallel\|\]
\[\vec{v}_\parallel = \vec{w}\frac{\vec{v}\cdot\vec{w}}{\|\vec{w}\|^2}\]
Se w já for um versor, a divisão é desnecessária. Para obter \(\vec{v}_\perp\) basta subtrair \(\vec{v}_\parallel\) de \(\vec{v}\). Essa projeção e decomposição de vetores serão bastante usadas não só para sombras, mas para computar tambeḿ a iluminação dos objetos de acordo com o sentido dos raios solares.
Antes de terminar esta seção, uma observação: podemos representar o produto escalar como uma multiplicação entre vetores. Dado os vetores coluna \(\vec{v}\) e \(\vec{w}\), então o produto escalar é:
\[\vec{v}\cdot\vec{w} = \vec{v}^T\vec{w}\]
Isso é importante quando formos trabalhar com multiplicação de matrizes.
Produto Vetorial
Existe uma outra operação que se mostrou bastante útil no mundo 3D. Esta operação resolve o seguinte problema: "Como posso achar um vetor que seja perpendicular a dois outros vetores?". O produto vetorial tem como resultado um vetor (daí o nome). A expressão para o produto vetorial é:
\[ \begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix} \times \begin{bmatrix} x_2 \\ y_2 \\ z_2 \end{bmatrix} = \begin{bmatrix} y_1z_2 - y_2z_1 \\ x_1z_2 - z_1x_2 \\ x_1y_2-y_1x_2 \end{bmatrix} \]
Parece confuso e aleatório? Vou dar uma dica para visualizar o padrão nessa multiplicação: para achar o primeiro valor do vetor resultante, remova a primeira linha dos dois vetores, junte os outros 4 números e calcule o determinante. Para o segundo ou terceiro valores, remova a segunda ou terceira linha e repita o processo. Daí podes lembrar: Isso se parece com determinante usando expansão em cofatores. Mas é isso mesmo, há uma forma de calcular esse produto vetorial usando apenas uma determinante. Se eu representar o vetor \([x,y,z]^T\) como \(x\vec{i}+y\vec{j}+z\vec{k}\), onde \(\vec{i} = [1,0,0]^T\), \(\vec{j} = [0,1,0]^T\) e \(\vec{k} = [0,0,1]^T\), então o produto vetorial pode ser representado como:
\[ \vec{v}\times\vec{w} = \begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \end{bmatrix} \]
O cálculo é o mesmo. Mas ainda há um problema:
- Que eu saiba, com dois vetores distintos, há outros dois vetores que são perpendiculares a eles. Qual deles é o resultado do produto vetorial?
Não conseguiu enxergar esses dois vetores? Vou mostrar:
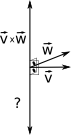
Lembras que a orientação na regra da mão direita é antihorária? E lembras da ordem polegar\(\rightarrow\)outros dedos\(\rightarrow\)palma da mão? Faça exatamente isso no produto vetorial:
- \(\vec{v}\times\vec{w}\): Polegar no v e os outros dedos no w. O vetor resultante do produto vetorial está saindo da palma da mão.
Mas quem é o outro vetor? Faça a mesma regra:
- \(\vec{w}\times\vec{v}\): Polegar no w e os outros dedos no v. O vetor resultante do produto vetorial está saindo da palma da mão.
Veja que um é o negativo do outro, ou seja:
\(\vec{v}\times\vec{w}\) = - \(\vec{w}\times\vec{v}\).
Essa é uma propriedade interessante. Outra propriedade interessante é com respeito à sua magnitude, pois ela é igual à área do paralelogramo formado pelos vetores \(\vec{v}\) e \(\vec{w}\):
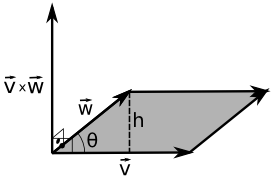
\[ \begin{split} Area_{paralelogramo} & = bh \\ & = \|\vec{v}\|h \\ & = \|\vec{v}\|\|\vec{w}\|sen(\theta) \\ & = \|\vec{v}\times\vec{w}\| \end{split} \]