Bem vindo à revisão de álgebra linear. Aqui irei mostrar o básico de álgebra linear, tentando . Esse tutorial foi feito visando os fundamentos para os tutoriais de WebGL, mas podem ser usados em qualquer outra aplicação.
Matrizes
Introdução
Uma matriz é um vetor multidimensional, retangular com valores dispostos em linhas e colunas. Uma matriz \(l\times c\) tem \(l\) linhas e \(c\) colunas. Podemos usar a notação \(M = [m_{ij}]\), onde \(1 \le i \le r\) e \(1 \le j \le c\), e \(m_{ij}\) representa o elemento na linha \(i\) e coluna \(j\). Uma matriz quadrada tem \(r = c\) (cuja dimensão chamarei de \(n \times n\)). A diagonal de matriz quadrada é um vetor [m_{ii}], onde \(1 \le i \le n\). Se apenas \(m_{ii}\) são não-nulos, então temos uma matriz diagonal. A matriz identidade é uma matriz diagonal onde \(m_{ii} = 1\) e os outros elementos são iguais a zero.
Você pode considerar os vetores como matrizes. O vetor linha é uma matriz \(1 \times n\), enquanto que o vetor coluna é uma matriz \(n \times 1\).
A transposta de uma matriz \(M_{l \times c} = [m_{ij}]\) é uma matriz \(M^T_{c \times l}=[m_{ji}]\), ambas com \(1 \le i \le l\) e \(1 \le j \le c\). Uma matriz é simétrica quando \(M = M^T\). A transposta de um vetor coluna é um vetor linha, e vice-versa. A transposta da transposta de uma matriz é igual à matriz.
Multiplicação de uma matriz por uma escalar
A multiplicação é semelhante à multiplicação entre vetores e escalares:
\[kM = k\begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33}\end{bmatrix} = \begin{bmatrix}km_{11} & km_{12} & km_{13} \\ km_{21} & km_{22} & km_{23} \\ km_{31} & km_{32} & km_{33}\end{bmatrix}\]
Multiplicação entre Matrizes
Poderíamos multiplicar as duas matrizes elemento a elemento, como por exemplo:
\[AB = [a_{ij}][b_{ij}] = [a_{ij}b_{ij}]\]
Inclusive nas ferramentas computacionais, existe essa operação de multiplicação elemento-a-elemento entre matrizes. Todavia, com o tempo, percebeu-se que uma outra forma de multiplicação se mostrava muito mais útil para o desenvolvimento da álgebra linear e suas aplicações. Mantendo a abordagem top-down, vou mostrar o conceito primeiramente mostrando um problema, um exemplo.
Imagine que estejas resolvendo um sistema de equações lineares:
\[ \begin{array}\\a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + a_{14}x_4 = b_1 \\ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 + a_{24}x_4 = b_2 \\ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 + a_{34}x_4 = b_3 \\ a_{41}x_1 + a_{42}x_2 + a_{43}x_3 + a_{44}x_4 = b_4 \end{array} \]
Podemos representar essas quatro equações como matrizes. Perceba que a primeira equação é um produto interno entre o vetor \([a_{11}, a_{12}, a_{13}, a_{14}]^T\) e o vetor \([x_1,x_2,x_3,x_4]^T\).
\[ \begin{array}\\[a_{11}, a_{12}, a_{13}, a_{14}][x_1,x_2,x_3,x_4]^T = b_1 \\ [a_{21}, a_{22}, a_{23}, a_{24}][x_1,x_2,x_3,x_4]^T = b_2 \\ [a_{31}, a_{32}, a_{33}, a_{34}][x_1,x_2,x_3,x_4]^T = b_3 \\ [a_{41}, a_{42}, a_{43}, a_{44}][x_1,x_2,x_3,x_4]^T = b_4 \end{array} \]
Podemos reunir as 4 equações:
\[ \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix}b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix} \]
Podemos abreviar as matrizes:
\[A\vec{x} = \vec{b}\]
Esse exemplo mostra uma multiplicação entre matriz e vetor. Percebeu que há uma relação entre as linhas da primeira matriz e as colunas da segunda matriz (que nesse caso só havia uma coluna, o vetor coluna)? O número de elementos dentro de cada linha do primeiro vetor e dentro de cada coluna do segundo vetor deve ser o mesmo. Generalizando, podes multiplicar vetores de diferentes tamanhos, porém seguindo essa regra.
\[A_{l \times n}B_{n \times c} = C_{l \times c}\]
Cada elemento de C pode ser computado da seguinte forma:
\[c_{ij} = \sum^{n}_{k=1}{a_{ik}b_{kj}}\]
Algumas observações com relação à multiplicação entre matrizes:
- Multiplicar uma matriz \(M\) por uma matriz quadrada \(Q\) (em qualquer um dos lados) mantém o tamanho de \(M\) (a multiplicação precisa ser válida);
Se \(I\) é a matriz identidade
\(MI = IM = M\);
Multiplicação de matrizes não é comutativa:
\(AB \neq BA\);
Multiplicação de matrizes é associativa:
\((AB)C = A(BC)\);
Associação também se rege com matrizes, escalares e vetores
\((kA)B = k(AB) = A(kB)\) e \((\vec{v}A)B = \vec{v}(AB)\)
A transposta de uma multiplicação é a multiplicação de transpostas, invertendo a ordem das matrizes
\((AB)^T = B^TA^T\).
Isso faz sentido quando levas em conta o tamanho das matrizes, de forma a manter a multiplicação válida:
\((A_{l \times n}B_{n \times c})^T = B^T_{c \times n}A^T_{n \times l}\)
Transposição da multiplicação pode ser estendido para mais de duas matrizes: \((M_1M_2 \cdots M_n)^T = M_n^T\cdots M_2^TM_1^T\)
Multiplicar um vetor e uma matriz
Lado esquerdo, lado direito, vetor coluna, vetor linha. Há 4 formas de multiplicar uma matriz e um vetor. Veja o que acontece mostrando exemplos com matrizes \(3\times 3\) e vetores:
\[ \begin{align} \begin{bmatrix}x & y & z\end{bmatrix}\begin{bmatrix}m_{11} & m_{12} & m_{13}\\m_{21} & m_{22} & m_{23}\\m_{31} & m_{32} & m_{33}\end{bmatrix} &= \begin{bmatrix}xm_{11} + ym_{21} + zm_{31} & xm_{12} + ym_{22} + zm_{32} & xm_{13} + ym_{23} + zm_{33}\end{bmatrix}\\ \begin{bmatrix}m_{11} & m_{12} & m_{13}\\m_{21} & m_{22} & m_{23}\\m_{31} & m_{32} & m_{33}\end{bmatrix}\begin{bmatrix}x \\ y \\ z\end{bmatrix} &= \begin{bmatrix}xm_{11} + ym_{12} + zm_{13} \\ xm_{21} + ym_{22} + zm_{23} \\ xm_{31} + ym_{32} + zm_{33}\end{bmatrix}\\ \begin{bmatrix}m_{11} & m_{12} & m_{13}\\m_{21} & m_{22} & m_{23}\\m_{31} & m_{32} & m_{33}\end{bmatrix}\begin{bmatrix}x & y & z\end{bmatrix} &= indefinido\\ \begin{bmatrix}x \\ y \\ z\end{bmatrix}\begin{bmatrix}m_{11} & m_{12} & m_{13}\\m_{21} & m_{22} & m_{23}\\m_{31} & m_{32} & m_{33}\end{bmatrix} &= indefinido \end{align} \]
Um vetor linha só pode ser multiplicado por uma matriz pelo lado direito, enquanto que um vetor coluna só pode ser multiplicado por uma matriz pelo seu lado esquerdo. O resultado é um vetor linha ou coluna respectivamente, mantendo a dimensão do vetor original. Outras observações:
- Cada elemento do vetor resultante é um produto escalar do vetor original com uma linha (para vetores coluna) ou coluna (para vetores linha) da matriz;
- Você pode imaginar os elementos \(m_{ij}\) como um peso do \(i\)-ésimo elemento do vetor original influenciando o \(j\)-ésimo elemento da saída (isso no caso da multiplicação com vetor linha). Com o vetor coluna, troque os papéis de \(i\) e \(j\). Ex (vetor coluna): \(m_{21}\) controla o quanto do valor de x contribui para o 2º elemento da saída.
Multiplicação é distributiva sobre adição de vetores:
\((\vec{v}+\vec{w})M = \vec{v}M + \vec{w}M\)
Agora perceba os valores da saída numa multiplicação com vetores linha:
\[\begin{bmatrix}xm_{11} + ym_{21} + zm_{31} & xm_{12} + ym_{22} + zm_{32} & xm_{13} + ym_{23} + zm_{33}\end{bmatrix}\]
Veja os valores da saída numa multiplicação com vetores coluna:
\[\begin{bmatrix}xm_{11} + ym_{12} + zm_{13} \\ xm_{21} + ym_{22} + zm_{23} \\ xm_{31} + ym_{32} + zm_{33}\end{bmatrix}\]
Independente do resultado ser um vetor coluna ou linha, os valores dos elementos não são os mesmos! Por isso a importância da distinção de um vetor coluna e um vetor linha. Como os livros de álgebra linear, bíblias de computação gráfica e o OpenGL utilizam vetores coluna, vamos seguir essa convenção. O DirectX utiliza vetores linha, e o raciocínio adquirido ao aprender os conceitos utilizando vetores coluna podem ser aplicados a vetores linha.
Interpretação Geométrica
Com tantas informações sobre matrizes, fiquei devendo ilustrações para entender as matrizes de uma forma visual, ao invés de apenas um grade de de números.
Como dito anteriormente nessa revisão, podemos representar um vetor como uma sequência de vetores ponderados:
\[ \begin{split} \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} & = 1\begin{bmatrix} v_1 \\ 0 \\ 0 \end{bmatrix} + 1\begin{bmatrix} 0 \\ v_2 \\ 0 \end{bmatrix} + 1\begin{bmatrix} 0 \\ 0 \\ v_3 \end{bmatrix} \\ & = v_1\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + v_2\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + v_3\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \\ & = v_1\vec{i} + v_2\vec{j} + v_3\vec{k} \\ & = \begin{bmatrix}\vec{i}&\vec{j}&\vec{k}\end{bmatrix}\begin{bmatrix}v_1\\v_2\\v_3\end{bmatrix} \\ & = \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}\begin{bmatrix}v_1\\v_2\\v_3\end{bmatrix} \end{split} \]
Nós expressamos o vetor \(\vec{v}\) como uma combinação linear dos vetores \(\vec{i}\), \(\vec{j}\) e \(\vec{k}\). Denominemos estes vetores como vetores base. Com estas bases, podemos formar qualquer vetor no espaço \(n\)-dimensional (\(n\) é o número de vetores base), todavia veja que não há combinação linear de \(\vec{i}\) e \(\vec{j}\) que resulte em \(\vec{k}\) (nem de \(\vec{j}\) e \(\vec{k}\) para \(\vec{i}\) e de \(\vec{k}\) e \(\vec{i}\) para \(\vec{j}\)). Quando isso acontece, então eles são linearmente independentes (LI). Existem diversas bases que podem formar o mesmo espaço vetorial, todavia elas precisam ser LI (nós denominamos os vetores base , e como base canônica). Se tiveres no seu conjunto de vetores base um vetor que seja combinação linear dos outros vetores, então sua base não é LI. É necessário remover esse vetor e fazer um novo teste, até conseguir um número de vetores base. Em 3D, a consequência de uma base LI de dimensão 3 é que seus três vetores não pertencem a um plano.
Então vamos representar geometricamente os vetores \(\vec{v}\), \(\vec{i}\), \(\vec{j}\) e \(\vec{k}\) (Em 2D é mais fácil de visualizar):

Se trocarmos a matriz identidade por uma outra matriz, por exemplo:
\[ \begin{bmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 5 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} = \begin{bmatrix} 2v_1 \\ 3v_2 \\ 5v_3 \\ \end{bmatrix} \]
Ou seja, o primeiro componente foi duplicado, o segundo foi triplicado e o terceiro foi quintuplicado. Então a matriz provoca uma transformação em um vetor. Generalizando, usando a mesma ideia do exemplo do sistema de equações, o resultado de uma transformação de uma matriz em um vetor é uma combinação linear dos elementos da matriz com os elementos do vetor.
Mas como eu sei que transformação uma dada matriz provoca? Você pode saber isso transformando os nossos vetores base canônicos.
\[ \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} m_{11} \\ m_{21} \\ m_{31} \end{bmatrix} \]
\[ \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} m_{12} \\ m_{22} \\ m_{32} \end{bmatrix} \]
\[ \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} m_{13} \\ m_{23} \\ m_{33} \end{bmatrix} \]
Então as colunas representam os vetores resultantes das transformações das bases canônicas. Por exemplo, em 2D, se a matriz for
\[ M = \begin{bmatrix} 2 & -1\\ 1 & 2\\ \end{bmatrix} \]
Significa que o vetor \(\vec{i}\) se transforma em \([2,1]^T\) e o vetor \(\vec{j}\) se transforma em \([-1,2]^T\). Vamos mostrar isso geometricamente:
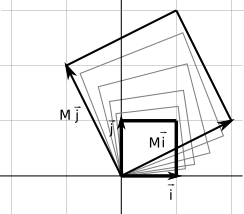
Então a transformação é uma espécie de escala e uma rotação. Significa que todos os vértices naquele espaço vão ser transformados dessa forma se multiplicados por esta matriz.
Algumas transformações podem ficar um tanto distorcidas. As transformações representadas por uma matriz são transformações lineares. Alguns tipos de transformações lineares são:
- Rotação
- Escala
- Projeção Ortográfica
- Reflexão
- Cisalhamento
Vamos abordar cada uma delas em detalhes.