Autor: Aléssio Miranda Júnior

ComplexidadeTeste

Aviso: Esta aula é puramente teórica e não é estritamente necessária para continuar o curso, caso o leitor não esteja entendendo bem a matemática usada, é recomendado que ele pule esta aula e volte quando estiver confortável com as notações matemáticas utilizadas.

Algoritmos e estruturas de dados são temas frequentemente ignorados por diversas pessoas da área de desenvolvimento e engenharia de software, desde universitários aos programadores mais experientes. Os principais argumentos utilizados giram em torno do fato de que “as linguagens de programação e frameworks atuais já implementam os algoritmos da maneira mais eficiente” ou de que “os recursos de hardware disponíveis hoje (como memória e processador) tornam a preocupação com algoritmos desnecessária”.

Hoje em dia também existe uma discussão muito recorrente sobre linguagens de programação serem melhores ou mais rápidas que outras. Apesar de uma poder ser melhor que outra em situações diferentes, de nada importa se a pessoa que estiver escrevendo o código não tiver uma noção fundamental de algoritmos.

Neste post falarei sobre o que é um algoritmo, a importância de estudá-los e apresentarei brevemente um dos temas mais importantes da Ciência da Computação para engenharia de software: Análise de Complexidade de Algoritmos.

Algoritmos

No mundo da ciência da computação, algoritmos são processos computacionais bem definidos que podem receber uma entrada, processá-la e produzir um ou mais valores como saída.

Alguns exemplos de problemas que envolvem algoritmos comuns são:

• Calcular a rota mais curta entre duas ruas
• Contar o número de amigos em comum em uma rede social
• Organizar de maneira eficiente tarefas de acordo com sua prioridade, prazo e duração
• Organizar a lista de contatos por ordem alfabética
• Encontrar uma mensagem no histórico de conversas

De forma geral, podemos pensar em algoritmos como uma ferramenta para resolver um problema bem definido. A definição de um problema se baseia em um conjunto de dados que se deseja processar, com suas especificidades, e o resultado que é desejado alcançar.

Como podemos perceber, existem diversos problemas que podem ser resolvidos utilizando algoritmos. Não existe uma “bala de prata” para resolvê-los de maneiras eficiente. Porém existem categorias nas quais os problemas e seus subproblemas podem ser classificados. Abstraindo o problema, podemos identificar a sua categoria e aplicar técnicas específicas conhecidas para resolvê-los da maneira mais eficiente.

Algumas das principais categorias/técnicas são:

• Greedy Algorithms
• Dynamic Programming
• Divide and conquer
• Backtracking
• Search and Sorting

Existem também Estrutura de Dados que são utilizados nessas e outras técnicas para ajudar na eficiência desses algoritmos. Como por exemplo: (Grafos, Árvores, Heaps, Tabelas Hash, Pilhas e Filas)

Eficiência dos algoritmos

Já sabemos que existem diversas ferramentas parar analisar a performance de um programa, os conhecidos Profilers. Porém, apesar de sua eficiência, eles não são úteis para Complexidade de Algoritmos. Complexidade de Algoritmos analisa um algoritmo em “nível de idealização/definição”— isto é, ignorando qualquer implementação de linguagens específicas ou hardware. Nós queremos comparar algoritmos em termos do que eles são: Ideias de como algo é computado.

Comparar o tempo que algoritmos levam para executar em milissegundos não são parâmetros para dizer que um algoritmo é melhor que o outro.

É possível que códigos mal escritos em Golang rodem muito mais rápido (até certo ponto) do que o mesmo código escrito em C# ou Java.

Vamos analisar duas soluções para o famoso problema Two Sum, que verifica se existem 2 números cuja soma resulte na entrada específica (alvo) e retorna as posições dos números encontrados:

func twoSum(nums []int, target int) (index1, index2 int) {
    for index1, _ := range nums {
        for index2, _ := range nums {
            if nums[index1]+nums[index2] == target {
                return index1, index2
            }
        }
    }
    return -1, -1
}

Algorítimo em Golang

fun twoSum(nums: IntArray, target: Int): Pair<Int, Int> {
    val seen = hashMapOf<Int, Int>()

    nums.forEachIndexed { index, value ->
        if (seen.contains(target - value)) {
            return Pair(seen[target - value]!!, index)
        }
        seen.put(value, index)
    }

    return Pair(-1, -1)

}

Algoritmo em Kotlin

Rodando as duas soluções com o arrays de até 1000 elementos, o algoritmo em Go é muito mais rápido que Kotlin, demorando apenas alguns nanosegundos para encontrar o resultado, enquanto Kotlin demora poucos milisegundos na maioria dos casos.

Será que podemos afirmar que o algoritmo em Go é melhor que o em Kotlin?

Para isso, precisamos definir o que realmente é um “algoritmo melhor”.

Podemos dizer que o melhor algoritmo para resolver um problema é aquele que possui a menor complexidade de tempo e espaço. Em outras palavras, é o algoritmo que, conforme a entrada cresce tendendo ao infinito, é aquele que apresenta a menor variação de tempo e memória utilizada para terminar.

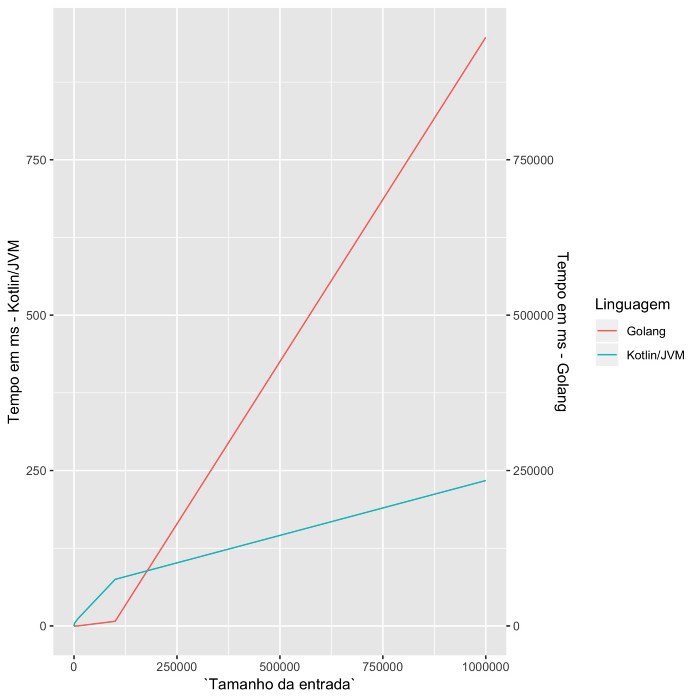
Rodando os mesmos algoritmos com entradas variando de 0 a 1 milhão e extraindo o tempo de execução podemos montar o seguinte gráfico:

diversas ferramentas

Conforme a entrada cresce, o tempo de execução em Kotlin varia muito pouco, apresentando valores entre 0 e 234 milisegundos. Já Go, apresenta tempos de execução entre 0 e 15 minutos com entradas muito grandes.

Um algoritmo pode ser melhor que outro quando processa poucos dados, porém pode ser muito pior conforme o dado cresce.

A Análise de complexidade nos permite medir o quão rápido um programa executa suas computações. Exemplos de computações são: Operações de adição e multiplicação; comparações; pesquisa de elementos em um conjunto de dados; determinar o caminho mais curto entre diferentes pontos; ou até verificar a presença de uma expressão regular em uma string.

Claramente, a computação está sempre presente em programas de computadores. Entender este conceito permitirá que continue estudando algoritmos com um melhor entendimento da teoria por trás deles.

Práticas de Exercícios Mundo do Código

Em geral os problemas nos dão um limite de 1 segundo para que o programa imprima a resposta, normalmente isso é equivalente a \(10^8\) operações simples em um computador (para sites e questões mais antigas esse valor pode ser menor). Vamos agora pensar então em como quantificar esse tempo gasto pelo programa para gerar uma saída. A ideia mais simples é usar o número de linhas de um programa, mas isso falha rapidamente, pois se usarmos alguma estrutura de repetição (como um for ou um while), uma das linhas será repetida várias vezes pelo programa, assim temos que os dois programas abaixo demoram tempos consideravelmente distintos.

    cin >> a >> b;
    c = a + b;
    cout << c;

    cin >> n;
    for(int i = 0; i < n; ++i){
        cin >> x[i];
    }

Código 1: Algorítimo em C++

Então podemos refinar um pouco nossa ideia, agora tentemos contar quantas linhas são executadas pelo computador, dessa forma podemos diferenciar muito bem os dois programas anteriores, pois para o computador eles são:

    cin >> a >> b;
    c = a + b;
    cout << c;

    cin >> n;
    int i = 0;
    cin >> x[0];
    i++;
    if(i >= n){
        break;
    }
    cin >> x[1];
    i++;
    if(i >= n){
        break;
    }
    cin >> x[2];
    i++;
    if(i >= n){
        break;
    }
    cin >> x[n - 1];
    i++;
    if(i >= n){
        break;
    }           

Que claramente têm uma quantidade diferente de linhas, o segundo inclusive tem uma quantidade variável. Porém, essa é a melhor medida que podemos usar? Se estamos atrás de precisão ela é bem ruim. Primeiro porque nem toda linha tem o mesmo custo num computador, adições são mais rápidas que multiplicações e estas são bem mais rápidas que tirar módulo. Além disso, tudo depende da arquitetura do computador, para alguns, checar memória é mais rápido que operações aritméticas, outros são otimizados para determinados tipos de multiplicação, uns reduzem o consumo de memória em troca de tempo, etc. Por outro lado todas essas variações são variações de constantes, então se quisermos aproximar de uma forma geral quanto tempo um programa demora rodando, devemos usar um método que ignora mudanças de constantes. Para este fim foram criadas as notações assintótica.

Quando analisamos assintoticamente um programa, nós nos preocupamos apenas com como o custo do programa varia a medida que sua entrada cresce, isso pode parecer meio simplista, por exemplo um programa que custa \(1000 \cdot \log(n)\) operações parece muito pior que um que custa \(n\) para um n pequeno, mas a medida que n cresce, o segundo algoritmos gasta bem mais tempo que o primeiro (para \(n = 10^6\), o primeiro consome em torno de 20000 operações, enquanto o segundo vai consumir 1000000 operações), assim vemos que é uma forma válida de análise.

Notação \(O\) (O-grande, Big-O)

A notação O-grande é uma das notações assintóticas mais comuns. A definição formal dela é a seguinte:

\(f(n) = O(g(n))\), se existe \(N\) e \(c\), tais que para todo \(n \geq N\), \(f(n) \leq c \cdot g(n)\).

Em sua definição já é fácil ver que ela ignora constantes, essa notação nos permite falar informalmente que uma função é menor que a outra, além de nos dar uma ótima noção de como o tempo gasto por um programa cresce com o n (e isso vai funcionar para qualquer computador independente de sua arquitetura).

Agora analisemos algumas propriedades dessa notação.

Propriedade 1:

Se \(f(n) = O(g(n))\), \(f + g = O(g(n))\).

Prova da propriedade 1:

Como temos \(f(n) = O(g(n))\), existe um \(c\) e um \(N\), tais que para todo \(n \geq N\), \(f(n) \leq c \cdot g(n)\). Tomando \(c_1 = c + 1\), conseguimos que para todo \(n \geq N\), $ c_1 g(n) = c g(n) + g(n) f(n) + g(n)$, que nos dá pela definição que \(f + g = O(g(n))\).

Propriedade 2:

Se \(f(n) = O(g(n))\) e sendo \(a\) e \(b\) são reais, \(a \cdot f + b \cdot g = O(g(n))\).

Prova da propriedade 2:

Como temos \(f(n) = O(g(n))\), existe um \(c\) e um \(N\), tais que para todo \(n \geq N\), \(f(n) \leq c \cdot g(n)\). Tomando agora \(c_1 = a \cdot c + b\) temos que a prova segue da mesma forma que a da propriedade 1.

Propriedade 3:

Se \(f_1(n) = O(g_1(n))\) e $ f_2(n) = O(g_2(n))$, então \(f_1 \cdot f_2 = O(g_1 \cdot g_2)\).

Prova da Propriedade 3:

Definamos \(c_1\), \(c_2\), \(n_1\), \(n_2\) de forma análoga à anterior, então se tomarmos \(c = c_1 \cdot c_2\) e \(n = \max(n_1, n_2)\), temos que: $ c g_1g_2 = (c_1g_1) (c_2g_2) f_1 f_2$ Sendo que a desigualdade é válida para n maior ou igual ao maior dentre \(n_1\) e \(n_2\), que foi como definimos \(n\), assim usando a definição da notação, a propriedade 3 é verdadeira.

Vejamos agora algumas vantagens e desvantagens da notação O-grande:

Vantagens

1. Analisamos apenas o que geralmente importa,ou seja qual algoritmo é melhor para valores elevados (de nada adianta ter um algoritmo rápido para n pequenos, porém para o n da questão ele é muito lento).
2. “Limpa” a notação. Em vez de escrevermos \(5\cdot n^3 + 12 \cdot n^{1/2}\), podemos simplesmente escrever \(O(n^3)\). Também em vez de usarmos \(n + log_2(n) + sen(n) + cos(n)\), podemos escrever simplesmente \(O(n)\).
3. Nos permite tentar da complexidade da solução do problema, o que nos permite ter uma noção dos algoritmos que usaremos para resolver a questão.
4. Manipulação de expressões ficam extremamente mais simples (todos os logaritmos são equivalentes). 5.Nosso problema com a arquitetura do computador é resolvido, pois nós ignoramos constantes.

Desvantagens

1. Às vezes uma função é assintoticamente mais rápida que outra, porém para os valores do problema é melhor usar a mais lenta. Por exemplo assintoticamente \((\log n)^4\) é “menor” que \(\sqrt n\), mas para n menor que \(2\cdot 10^{12}\) \(\sqrt n\) é menor que \((\log n)^4\), e portanto para uma questão com n menor que esse valor, seria melhor usar o segundo algoritmo.

2. Em alguns casos os fatores menores e as constantes podem realmente lhe fazer receber um TLE (Time Limit Exceeded), em especial em questões com tempos limites muito estritos.

3. Por vezes a solução real do problema é lenta e não devia passar no tempo, porém devida a alguma estrutura na entrada não especificada na entrada da questão permite que o problema passe, ou talvez a solução certa tenha uma complexidade alta e você deve usar heurísticas para tornar o programa mais rápido.

Agora analisemos agora algumas complexidades, em ordem de “menor” para “maior”.

\(O(1)\)

    // Um algoritmo que sempre vai demorar a mesma 
    // quantidade de tempo, independente da entrada,
    // ou seja, de tempo constante.
            
            cin >> a >> b;
            c = a + b;
            cout << c;

\(O(\log(n))\)

Esse algoritmo custa uma quantidade de operações proporcional ao logaritmo do número, assim se elevamos n ao quadrado, duplicamos o tempo necessário para o algoritmo gerar resposta, o algoritmo mais conhecido nessa complexidade é a busca binária, e o mais simples é tirar a parte inteira do logaritmo de um número.

            
            //busca nos dígitos binários do número
            //não é uma busca binária
            //imprime a parte inteira da raiz de n
            int n, sq = 0, test;
            cin >> n;
            for(int pot = 31; pot >= 0; --pot){
              test = sq + (1 << test);
              if(test*test <= n)  sq = test;
            }
            cout << sq << "\n";

\(O(\sqrt n)\)

Um algoritmo que cresce como a raiz do próprio n, assim se multiplicamos n por quatro, esse programa demora 2 vezes a mais que antes.

            // calcula a parte inteira da raiz de n
            int n, sq;
            cin >> n;
            for(sq = 1; sq*sq <= n; ++sq);
            --sq;
            cout << sq << "\n";

\(O(n)\)

Conhecido como linear. Geralmente um loop que vai de 0 a algum múltiplo fixo de n.

            
            cin >> n;
            for(int i = 0; i < n; ++i){
              cin >> x[i];
            }

\(O(n \cdot \log(n))\)

Os algoritmos primeiramente encontrados nessa categoria são as ordenações rápidas por comparação (quicksort, merge-sort, etc).

            //ordenação usando a STL
            int n, v[100000];
            cin >> n;
            for(int i = 0; i < n; ++i){
              cin >> v[i]; //custa O(n)
            }
            sort(v, v + n); //ordena o vetor, custa O(nlog(n))
            //n + nlog(n) = O(nlog(n))

\(O(n^2)\)

Conhecidos como algotitmos quadráticos, o programa demora tempo proporcional ao quadrado do n. Dessa forma se duplicamos o n, o tempo fica quatro vezes maior. Qualquer código que tenha que ler/preencher uma matriz quadrado de dimensão n custo pelo menos isso.

            //ler as entradas de uma matriz
            int n, G[1000][1000];
            for(int i = 0; i < n; ++i){ //Temos O(n*custo do for interno)
              for(int j = 0; j < n; ++j){ //Termos O(n*operação do for)
                cin >> G[i][j]; //O(1)
              }
            }
            //Assim a complexidade é O(n*O(n*(O(1)))) = O(n^2)

\(O(2^n)\)

Conhecida como classe exponencial, os algoritmos dessa classe geralmente são força bruta. Normalmente esses algoritmos têm que percorrer todos os subconjuntos de um conjunto de n elementos.

            
    //Soma de conjunto, O(n*2^n)
    int n, v[20], m;
    cin >> n >> m;
    for(int i = 0; i < n; ++i){
        cin >> v[i]; //leitura, O(n)
    }
    
    for(int mask = 0; mask < (1 << n); ++mask){ //passa por todos os subconjuntos O(2^n)
        int soma = 0;
        for(int i = 0; i < n; ++i){ //loop O(n)
            if((1 << i)&mask){ //checa se um elemento está nesse subconjunto
                soma += v[i];
            }
        }
        if(m == soma){
        for(int i = 0; i < n; ++i){
            if((1 << i)&mask){
                cout << i << " ";
            }
        }
        cout << "\n";
        break;
        }
    }

\(O(n!)\)

Algoritmos que rodam em tempo proporcional ao fatorial, normalmente algoritmos dessa classe são força bruta. Um exemplo é o cacheiro viajante por força bruta.

    //Checar a posição lexicogŕafica de uma ordem de um vetor, O(n * n!)
    int n, v[10], u[10], ans, stop;
    cin >> n;
    for(int i = 0; i < n; ++i){
        cin >> v[i]; //leitura, O(n)
    }
    for(int i = 0; i < n; ++i){
        u[i] = v[i]; //copio o vetor para outro, O(n)
    }
    sort(u, u + n) //ordenação, O(nlog(n))
    for(ans = 0; 1; ++ans){
        stop = 0;
        for(int i = 0; i < n; ++i){ //checa se os vetores são iguais, O(n)
            if(u[i] != v[i])  break;
            if(i == n - 1)  stop = 1;
        }
        if(stop){
            break;
        }
        next_permutation(u, u + n); //transforma o u na próxima ordenação do vetor na ordem lexicográfica, pode se repetir n! vezes
    }
    cout << ans << "\n";

Por fim, vejamos algumas simplificações de expressões usando nossa notação, e algumas questões de aplicação.

Exemplo 1: \(O(\sqrt n + n^2 + n^3 + n \log(n)) = O(n^3)\)

Exemplo 2: \(O(n^q+ \log(n)) = O(n^q)\), para qualquer q maior que 0.

Exemplo 3:\(O(a^n + n^b) = O(a^n)\), para quaisquer constantes a e b com a maior que 1.

Questão 1: Dê a notação O simplificada da seguinte expressão: \(\cos(n) + 1000 \cdot n + n^2\).

Questão 2: Temos uma questão cuja entrada é um número n, você conseguiu uma solução \(O(\sqrt n)\), qual o maior valor de n para o qual você tem certeza (supondo um juiz moderno e constante pequena) que seu programa vai passar?

Questão 3: Você se deparou com um problema onde você deve fazer uma busca binária em cada um dos subconjuntos de um conjunto de n elementos, qual a complexidade assintótica (notação O) desse algorítimo

Exercícios Sugeridos